 Technology Notebook Contents
Technology Notebook ContentsEffective Date: 1 September 98
Previous ~~ Next
by
Harold K. Cheney
Douglas Aircraft Company
McDonnell Douglas Corporation
Long Beach, California
Distance and velocity data to calculate takeoff and landing performance can be obtained from aircraft's Inertial Reference System's (IRS) component velocities, its radio altitude, and runway slope data. No external tracking information obtained from lasers, phototheodolites or belly-cameras is necessary. External information is needed on runway slope. Performance data thus obtained are superior or equivalent to data from external systems. The equations and procedures for using IRS data are presented.
Douglas Aircraft Company's experience in using distance and velocity data from inertial reference systems to calculate takeoff, rejected takeoff, landing, and taxiing maneuvers began in 1976 during the YC-15 STOL Transport Flight Test Program (References 1 and 2). The Litton LTN-l5 Inertial Navigation System provided the necessary data, and the results were satisfactory. Following this initial success, the IRS tracking procedures were then applied to MD-80 and DC-10 flight tests. The procedures were refined and combined with others to provide wind and ambient temperatures without using external instrumentation (References 3 and 4).
The basic equations for calculating distance, height, velocity, and acceleration have not been changed since the their use on YC-l5 program. Accuracy of distance and height measurements have been improved by using increased update rates of the component velocities, The accuracy-of-height measurement has been improved by an increase of the barn-loop time constant used to determine vertical velocity. This was made possible by the use of the Litton LTN-96 strapdown laser gyro inertial system in 1985 (Reference 4).
This action of the Society of Flight Test Engineers (SFTE) Technical Notebook describes requirements and procedures for obtaining tracking data using IRS information. The equations are those used in the Douglas Aircraft Test and Certification Flight Test Aerodynamic Performance Computer Program - X5AB (Reference 5). Additional information is available in References 6 through 9. Reference 6 provides a complete overview of trajectory measurements for flight test activities.
The primary sources of information used by the IRS tracking procedures are the IRS unit's three orthogonal velocities: north, east, and vertical. During normal IRS operation, the velocity values wander slowly around the true values. Therefore, it is necessary to provide some system to adjust the indicated values to true values for the period of the teat. For north and east velocities, this is accomplished by including a stationary period immediately before or after the test. For vertical velocity, the required correction is obtained by comparing the height values calculated from IRS vertical velocity with calculated height values from an alternate source. The alternate source values for takeoff are height values calculated from runway slope data prior to liftoff. The reference value for landing is the radio altitude prior to touchdown corrected for pitch attitude and runway slope. The calculated distance and height values must be adjusted to the desired reference location for the test maneuver (e.g., brake release, liftoff, touchdown or stop). The procedure which provides the time of these events will depend on the instrumentation on the test air craft. In summary, the information needed to calculate tracking data are the three IRS velocities, a stationary period, runway slope, radio altitude, pitch attitude, and procedures to establish the reference events.
 VELOCITY AND DISTANCE CALCULATION
VELOCITY AND DISTANCE CALCULATION
The following equations are used to calculate speed, distance. and height using IRS component velocities:
VN = VNI + CVN
VE = VEI + CVE
VV = VVI + CVV
VG = SQRT[(VN)2 + (VE)2]
VFP = J(VN)2 + (VE)2 + (VV/1.6878)2
X = SUMMATION[(INT) [1.6878(VG(i-1)+VG(I))/2]
SG = X-Xref
DZ = 2(LINS) x sin(90-0/2-AINS) sin(0/2)
ZTins = SUMMATION[(INT)(VVi..1 + VVi)/2 -DZ
Z = ZTins - ZTinsref
where:
VN = North velocity
VE = East velocity
VV = Vertical velocity
VNI, VE1, and VVI = Indicated component velocities
CVN, CVE, and CVV = Velocity corrections
VG = Ground speed
VFP = Flight path velocity
X = Initial distance calculation
(Sigma) = Sum of increments
INT = Calculation interval
1.6878 = Conversion of knots to feet per second
VGi-1 = Ground speed of previous calculation
VGi = Ground speed of current calculation
SG = Final distance
Xref = Calculated distance at reference time
DZ = IRS height change due to degree of pitch attitude
LINS = Distance from IRS to main gear tire contact
0 = Aircraft pitch attitude
AINS = Angle from pitch attitude reference line to line from IRS to tire contact
ZTins ref = Initial high calculation
VVi-1 = Vertical velocity of previous calculation
VVi = Vertical velocity or current calculation
Z = Final height
ZTins = Calculated height at reference time
 NORTH AND EAST VELOCITY CORRECTIONS
NORTH AND EAST VELOCITY CORRECTIONS
The indicated values of IRS north and east velocities wander around the true values at a period of approximately 84.4 minutes. This is known as the Schuller effect. Typical component velocity errors during takeoff and landing operations for the LTN-51 INS are shown in Figure 1. These values were obtained with the aircraft stationary either before takeoff or following a landing. The corrections. CVN and CVE, are the values which will bring the VNI and VEI values to zero during the stationary period of the calculation. If a stationary period is not available accurate position data cannot be calculated. (Note: Some users have developed external systems which measure velocity or distance during a portion of a maneuver to provide a correction to the indicated velocity and distance values along the aircraft path. References 6 and 7).
The correction values, CVN and CVE, are assumed to be constant during the test, which is true when the velocity errors are at their maximum values. As the velocity error value crosses zero, it may change as much as 0.2 knot in 60 second.


The correction for the variation between indicated vertical velocity and true vertical velocity value is more complicated. The correction value is determined from an initial calculation using indicated values. The initial height values are then compared to the height values calculated from either runway slope or radio altitude data. The procedure for comparing the height values using their difference as shown in Figures 3 and 4. The initial calculation is made using a CVV value of zero and the runway slope value known to exist in the vicinity of liftoff. A typical result of an initial calculation is shown in Figure 3. The break in the INS height during the round roll is due to the change in runway slope.
To determine the CVV value, a plot of the difference between the two height values is made as shown in Figure 4. The slope of the difference values is used to determine the CVV adjustment. The time of the break in the difference is loaded for the calculation of running height using the two runway slopes during the next calculation. The final height result, from the two sources is shown in Figure 5. The data for Figures 3 through 5 came from LTN-5l data using the period prior to rotation as the reference.




Experience has proven that the best height reference source for takeoff is runway slope data prior to lift off as shown in Figures 3, 4, and 5. For takeoffs with climb out pitch attitude less than 12 degrees. IRS height agrees with both the runway slope and radio altitude height values. For takeoffs at a higher pitch attitude, it appears the radio altitude values are not correct. This phenomena is confined in Reference 6. For landing, the best reference source is radio altitude corrected for pitch and runway slope. After touchdown, the IRS height values do not appear to be valid. The IRS vertical velocity values appear to be changed by the touchdown jolt and braking deceleration.
To provide reference height information for IRS height data and to obtain correct radio altitude height, the height change of the runway must he known. Very few runways are truly level. For example, the runway in Yuma. Arizona. used by Douglas for much of its testing, has three distinct slopes. The runway height calculation requires a survey of the runway slope and the location of change in the slope. The basic equation for calculation runway height (Zrwy) is:
Zrwy = SG x RWYSLP
where:
Zrwy = Height of runway relative to height reference
SG = Distance from height reference location
RWYSLP = Slope of runway (1 foot in 1,000 feet = 0.00l)
If the runway has more than one slope, more equations are needed. For takeoff on a runway with three slopes, the equations become:
Prior to slope change,
BZrwy = SG x RWYSLP1
During second slope,
Bzrwy = SG2 x RWYSLP1 + (SG-SG2) x RWYSLP2
Following start of third slope
BZrwy = SG2 x RWYSLP1 + (SG3-SG2) x RWYSLP2 + (SG-SG3)x RWYSLP3
Final value
Zrwy = BZrwy - BZrwylo
where:
BZrwy = Height of runway with respect to brake release
SG = Distance from reference location (brake release)
RWYSLPI = First slope value
SG2 = Distance from reference to start of second slope
RWYSLP2 = Second slope value
SG3 = Distance from reference to start of third slope
RWYSLP3 = Third slope value
Zrwy = Height of aircraft in respect to liftoff location
Bzrwylo = Value of BZrwy at liftoff
Before the Zrwy calculation the value of SG is stored as a data array versus time. The values of RWYSLPI, RWYSLP2, RWYSLP3, and the time of the slope changes are provided by the run input record. The SG2 and SG3 values are determined using the SG data array and the times of slope changes. The time of the slope changes are determined by the jump of vertical velocity values in the rime history of the IRS test data. An example of this jump is discussed in the section entitled "Baro-Inertial Loop Time Constant."
A similar set of equations is used for landing calculations, except that Zrwy is calculated directly instead of BZrwy. This is possible because touchdown is the reference location for both distance and height.
 RADIO ALTITUDE HEIGHT CALCULATIONS
RADIO ALTITUDE HEIGHT CALCULATIONS
To provide correct height information from radio altitude v4lues requires adjustment for pitch attitude and runway slope. Figure 7 is a graphical presentation of the geometry involved in calculating the height or the aircraft above a horizontal plane through the reference height location using indicated radio altitude. The height is calculated by the following equations:
ZTrad = Hrad - DZrad (O -Oref)
ZTradref = f(trefZTrad
Zrad = ZTrad - ZTradref + Zrwy
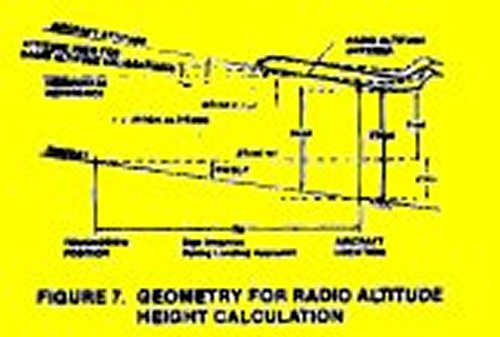
where:
ZTrad = Radio attitude corrected for pitch attitude
Hrad = Indicated radio altitude height
DZrad = Height correction per degree of pitch attitude
O = Aircraft pitch attitude
Oref = Pitch attitude used for radio altitude calibration
ZTradref = ZTrad value at reference event time
f = Function (ZTrad at tref event time)
tref = Time of reference event (liftoff or touchdown)
Zrad = Final radio altitude height value
Zrwy = Runway height calculated using runway slope
(NOTE: In Figure 7. the value is negative)
The values of indicated radio altitude (Hrad) and pitch attitude (0) are obtained from data arrays of the recorded test data. The correction of height for pitch attitude (I)Zrad) and pitch attitude used for radio altitude calibration (Oref) arc aircraft constants depending on the geometry of the aircraft. The reference event time (or liftoff and touchdown must be obtained from instrumentation other than IRS or radio altitude. (e.g., wheel speed anti- skid voltage. accelerometers, or strain gages on the landing structure).
The above equations are used after liftoff and prior to touchdown. To provide a similar reference for IRS height when the aircraft is on the runway, an alternate calculation using runway slope values is used. To provide continuity for the reference data, the same parameter name and number are used. The following is the alternate equation:
Zrad = Zrwy - MGext
where:
Zrad = Aircraft height in respect to reference height
Zrwy = Runway height in respect to reference height location
MGext = Vertical distance from bottom of tire with weight on the wheels to bottom of uncompressed tire with shock strut extended
 POSITION COORDINATE CALCULATIONS
POSITION COORDINATE CALCULATIONS
The basic equations presented in the "Velocity and Distance Calculation" section provide distance and velocity along the aircraft path. To provide coordinate position information similar to that provided by laser or photo theodolite systems requires another set of equations. The equations provide a distance along a reference direction and a distance perpendicular to that reference line. They are valuable for measuring lateral distance during ground minimum control speed (VMCG) tests, minimum turning radius taxi tests, and the space required for flight maneuvers. The following equations provide X and Y velocity and distance values:
VHD = VN x cosRD + VE x sinRD
VLAT = VE x cosRD - VN x sinRD
X = SUMMATION[(INT)1.6878 (VHDi..1 + VHDi)/2]
Y = SUMMATION[(INT)l.6878(VLATi..1 + VLATi)/ 2]
where:
VHD = Velocity along the reference direction (knots)
VN = Corrected north velocity
RD = Reference direction (angle from true north)
VE = Corrected east velocity
VLAT = Velocity perpendicular to the reference direction
X = Distance parallel to the reference direction line
Y = Distance perpendicular to the reference line
SUMMATION(i..1) = Sum of increment values
INT = Calculation interval (seconds)
1.6878 = Conversion of knots to feet per second
VHDi-1 = Previous value of YHD
VHDi = Current value of VHD)
VLATi-1 = Previous value of YLAT
VLATi = Current value of VLAT
The values of VN and VE are obtained using the same procedure presented in the "Velocity and Distance Calculation" section. The reference direction (RD) is normally the true heading of the runway. The values of X and Y obtained by the equations shown are from the start of the calculation run. If values from a reference event are desired, they can be obtained by subtracting Xref and Yref values as done for the X and Z values in the basic equations.
When a stationary period is not available to provide CVN and CVE values, the resulting lateral information can be adjusted to probable correct values, by adjusting the reference direction (RD) in a subsequent calculation. If it is known that an aircraft was relatively close to the centerline of the runway when a lateral distance of 100 feet is calculated for a distance 10,000 feet down the runway, a more correct lateral value can be calculated by adjusting the RD value input on the run record. In this case, the RD value would be adjusted by the angle increment of the tangent of 100/10,000. An example of this type of adjustment is presented in Figure 8 (Reference 10).

 BARO-INERTIAL LOOP TIME CONSTANT
BARO-INERTIAL LOOP TIME CONSTANT
The use of greater baro-inertial loop time constant values with the LTN-96 units has resulted in a major improvement in the determination of INS height for takeoff and landing performance. Previously, it had not been possible to obtain consistent agreement between laser. phototheodolite. radio altitude, runway slope, and INS height values. Now, good agreement has been obtained between INS height and runway-slope/radio-altitude height values for a number or takeoff and landing runs. The agreement shown for adjusted values in Figure 6 is typical.
The improvement obtained between the LTN-5l with a time constant of 50 seconds and the LTN-96 with a 150-second value is demonstrated by the result from a rejected takeoff test during which data from both systems were obtained. Figure 9 compares the INS height values using a ISO-second time constant with those calculated from runway slope during the run and presents the difference between the two values. A vertical velocity error of 0.1 foot-per-second was developed during the run as shown by the rate or change of height after stop. The versus data plotted versus distance instead of time are shown in Figure 10. The difference is only 2 feet over a 8,000-foot run.


The vertical velocity values provided by the LTN-96 during the test are shown in the top area of Figure 11. Because or aircraft jostling, the values vary from minus 1 foot-per-second to plus 1 foot-per-second. The shift of values at the runway dip is evident. It is this jump of vertical velocity value which Is used to determine the time of runway slope change discussed in "Runway Height Calculations." In the bottom section of Figure 11 the reference pressure altitude and INS damped altitude are shown. Pressure altitude following stop is 2 feet greater than before brake release. This agrees with the 2-foot gain shown by the runway slope height calculation presented in Figures 9 and 10. The INS damped altitude decreases 8 feet because of the baro- inertial loop action to adjust INS altitude to match pressure altitude. The same action changed INS indicated vertical velocity from plus 0.2 to 0.1 during the run and caused the 0.1-foot-per-second slope of height values following stop in Figure 9.
Results from the same run using the LTN-5l data are shown in Figure 32. The calculation for the data shown used a CVV value set to show the dip that was experienced during the middle of the run. The improvement is obvious. If the CVV value had been set to provide a constant height prior to brake release, the LTN-51 value at stop would have been minus 35 feet.


Frequently, the three velocity components are not available from production IRS units in an aircraft. It is still possible to obtain an approximate distance and height data using the indicated ground speed and radio altitude. This can be accomplished using the following equations:
VG = VGI + CVG
X = SUMMATION[I..1(INT)1.6878 (VGi..1 + VGi)/2]
SG = X - Xref
Z = Zrad
where:
VG = Adjusted ground speed
VGI = Indicated ground speed
CVG = Ground speed correction
SG = Distance from reference location
X = Calculated distance
Z = Height
Zrad = Calculated radio altitude value adjusted for pitch attitude and runway slope
If the indicated ground speed is zero during the stationary period of the test run, the distance values are valid. If a velocity value exists at zero round speed, it can be used to determine a CVG value. Then, two calculations can be made using both positive and negative sign for the CVG value. One of the two distances will be valid. This condition is because the sign of the error is unknown. Indicated radio altitude will be valid if the runway is level or has only one slope. Without vertical velocity, the time of change of slope cannot be determined. The radio altitude values will probably have a plus or minus one root accuracy due to the scatter characteristics of radio altitude measurement. The scatter is normally not apparent unless the radio altitude values are compared with IRS height values, or a detail review is made of the height increments for short periods of time during the test maneuver (0.2 second).
If a stationary period does not exist. it is still possible to obtain distance data if some other source of velocity is known for a period of time during the run (e.g. ground speed from the voltage indication of the wheel brake anti- skid system). This procedure has been used for autoland test data when it is undesirable to use the time to come to full stop. This process is presented in Reference 10.
Inertial Rererence System (IRS) component velocity data are a source of velocity and position data for takeoff and landing performance flight testing.
To use IRS velocity data for tracking information requires some procedure to adjust the indicated values to true values.
To obtain accurate height data requires knowing the runway slope and having radio altitude data available.
BZrwylo = Value of BZrwy at liftoff
|
Zrwy = Height or runway relative to height reference
|
 REFERENCES
REFERENCES
2. Cheney, Harold K., "Analysis Methods and Computer Programs Developed for YC-15 STOL Flight Test
Program," Douglas Paper 6635, AIAA Aircraft Systems
Technology Mating, Seattle. Washington, August 1977.
3. Cheney, Harold K., "Takeoff Performance Data Using Onboard Instrumentation," Douglas Paper 7339, SFTE Annual Symposium. Newport Bench, California, August 1983.
4. Cheney. Harold K., "Onboard Instrumentation for Flight Test Takeoff Performance," Douglas Paper 7675, ISA Aerospace Test Measurement Symposium, Seattle, Washington, May l986.
5. Chency, Harold K., "A Flexible Computer Program for Aircraft Flight Test Performance," AIAA 88-2125, MDC Report 33948, AIAA 4th Flight Test Conference, San Diego, California, May 3988.
6. Pool, A., d'Agut, P. deBenque, Riebeek, H.. "Trajectory Measurements for Take-off and Landing Tests and Other Short-Range Applications," AGARDograph No. 160. Volume 16 of AGARD Flight Test Instrumentation Series, January 1955.
7. Pool, A., Simmons. J. L., Wamsiak, G.J.H., and Willekens, A.J.L., "A Method for Measuring Takeoff and Landing Performance of Aircraft Using an Inertial Sensing System," National Aerospace Laboratory Report W0360." AGARD Flight Mechanics Panel Symposium, Gaillo, Norway, October 1980.
8. Van der Veen. J.C.Th., "Trajectory Measurement of the Fokker 100 Aircraft during Autoland Testing." National Aerospace Laboratory. NLR, ISA 32nd International Instrumentation Symposium, Seattle, Washington, 1986
9. Parlini, Frank, "Applications of Inertial Systems as Flight Test Sensors," Boeing Commercial Airplane Co.," AIAA Second Flight Test Conference, Las Vegas, Nevada. November 1983.
10. Cheney. Harold K. and Canh. T., "A New Test Method to Confirm Category III Auto land Performance," AIAA 88-2126. Douglas Paper No. 7964, AIAA Flight Test Conference, San Diego, California, May 1988.
Table of Content ~~ Previous ~~ Top ~~ Next